GEOMETRIA ESPACIAL "VOLUME DO PRISMA"

Amigo leitor segue pra seu conhecimento aumentar cada dia mais, volume do Prisma...

Generalização do volume de um prisma

      Para obter o volume de um prisma, vamos usar o princípio de Cavalieri ( matemático italiano, 1598 - 1697), que generaliza o conceito de volume para sólidos diversos.

      Dados dois sólidos com mesma altura e um plano , se todo plano, paralelo a , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais:

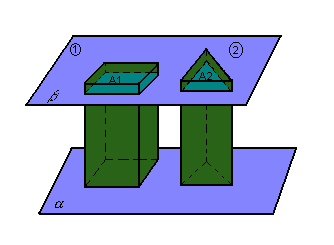        Se 1 é um paralelepípedo retângulo, então V₂ = A_Bh.

       Assim, o volume de todo prisma e de todo paralelepípedo é o produto da área da base pela medida da altura:

Vprisma = ABh

Cilindro
      Na figura abaixo, temos dois planos paralelos e distintos,, um círculo R contido em e uma reta r que intercepta , mas não R:

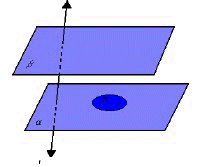
      Para cada ponto C da região R, vamos considerar o segmento , paralelo à reta r :

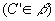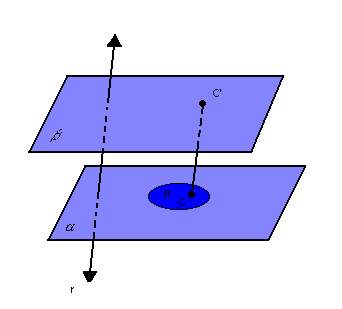
      Assim, temos:

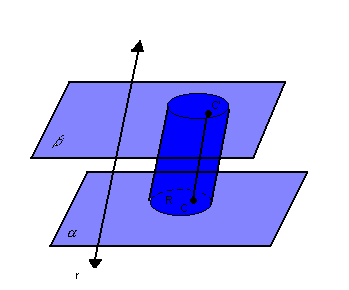
      Chamamos de cilindro, ou cilindro circular, o conjunto de todos os segmentos congruentes e paralelos a r.

   
Elementos do cilindro

      Dado o cilindro a seguir, consideramos os seguintes elementos:

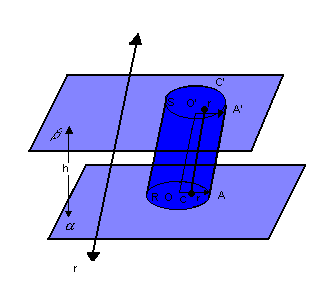
• bases: os círculos de centro O e O'e raios r
• altura: a distância h entre os planos
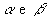
• geratriz: qualquer segmento de extremidades nos pontos das circunferências das bases ( por exemplo, 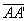) e paralelo à reta r.
  
  
  Aproveitem para aperfeiçoar sempre mais...!!!