Um número é considerado divisível por outro quando o resto da divisão entre eles é igual a zero. Para que a divisão entre os números resulte em partes inteiramente iguais, necessitamos ter conhecimento sobre algumas regras de divisibilidade.
Regras de Divisibilidade
Divisibilidade por 1
Todo número é divisível por 1.
Divisibilidade por 2
Todo número par é divisível por 2, isto é, todos os números terminados em 0, 2, 4, 6 e 8.
12:2 = 6
18:2 = 9
102:2 = 51
1024:2 = 512
10256:2 = 5128
Divisibilidade por 3
Um número é divisível por 3 quando a soma de seus algarismos constitui um número divisível por 3. Exemplo:
66 : 3 = 22, pois 6 + 6 = 12
60 : 3 = 20, pois 6 + 0 = 6
81 : 3 = 27, pois 8 + 1 = 9
558 : 3 = 186, pois 5 + 5 + 8 = 18
Divisibilidade por 4
Se os dois últimos algarismos de um número forem divisíveis por 4, então o número é divisível por 4. Para ver se os dois últimos algarismos formam um número divisível por 4, basta verificar se o número é par e sua metade continua par. Os números que possuem zero nas suas últimas duas casas também são divisíveis por 4.
288 : 4 = 72, 88 é par e a sua metade será par.
144 : 4 = 36, 44 é par e sua metade será par.
100 : 4 = 25, pois possui na última e penúltima casa o algarismo 0.
Divisibilidade por 5
Todo número terminado em 0 ou 5 é divisível por 5.
10:5 = 2
25:5 = 5
75:5 = 15
200:5 = 40
Divisibilidade por 6
Constitui todos os números divisíveis por 2 e 3 no mesmo instante.
42 : 6 = 7, pois 42 : 2 = 21 e 42 : 3 = 14
54 : 6 = 9, pois 54 : 2 = 27 e 54 : 3 = 18
132 : 6 = 22, pois 132 : 2 = 66 e 132 : 3 = 44
570: 6 = 95, pois 570 : 2 = 285 e 570 : 3 = 190
Divisibilidade por 7
Duplicar o algarismo das unidades e subtrair do resto do número. Se o resultado for divisível por 7, o número é divisível por 7. Exemplo:
203 : 7 = 29, pois 2*3 = 6 e 20 – 6 = 14
294 : 7 = 42, pois 2*4 = 8 e 29 – 8 = 21
840 : 7 = 120, pois 2*0 = 0 e 84 – 0 = 84
Divisibilidade por 8
Todo número será divisível por 8 quando terminar em 000, ou os últimos três números forem divisíveis por 8. Exemplo:
1000 : 8 = 125, pois termina em 000
1208 : 8 = 151, pois os três últimos são divisíveis por 8
Divisibilidade por 9
É todo número em que a soma de seus algarismos constitui um número múltiplo de 9. Exemplo:
90 : 9 = 10, pois 9 + 0 = 9
1125 : 9 = 125, pois 1 + 1 + 2 + 5 = 9
4788 : 9 = 532, pois 4 + 7 + 8 + 8 = 27
Divisibilidade por 10
Todo número terminado em 0 será divisível por 10
100:10 = 10
50:10 = 5
10:10 = 1
2000:10 = 200
Divisibilidade por 11
Um número é divisível por 11 nas situações em que a diferença entre o último algarismo e o número formado pelos demais algarismos, de forma sucessiva até que reste um número com 2 algarismos, resultar em um múltiplo de 11. Como regra mais imediata, todas as dezenas duplas (11, 22, 33, 5555, etc.) são múltiplas de 11.
1342 : 11 = 122, pois 134 – 2 = 132 → 13 – 2 = 11
2783 : 11 = 253, pois 278 – 3 = 275 → 27 – 5 = 22
7150: 11 = 650, pois 715 – 0 = 715 → 71 – 5 = 66
Divisibilidade por 12
São os números divisíveis por 3 e 4.
276:12 = 23, pois 276:3 = 92 e 276:4 = 69
672 : 12 = 56, pois 672 : 3 = 224 e 672 : 4 = 168



.jpg)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg) , em que k é uma constante de proporcionalidade.
, em que k é uma constante de proporcionalidade..jpg)
.jpg)
.jpg)
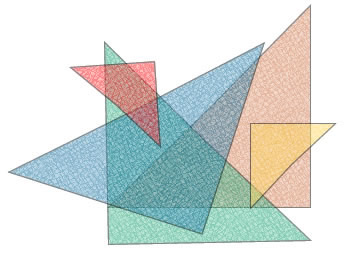

.jpg) ,
, .jpg) C, B?A, BÂC.
C, B?A, BÂC.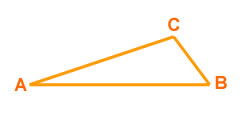
.jpg)



.jpg)

.jpg)



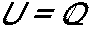 , resolva a equação
, resolva a equação 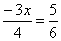 .
.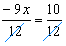
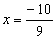
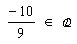 , então
, então 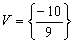 .
.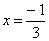
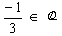 , então
, então 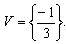
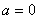 e
e